LeetCode热题100（简单/中等）—— 链表

1 相交链表

难度：简单

题目描述

给你两个单链表的头节点 headA 和 headB ，请你找出并返回两个单链表相交的起始节点。如果两个链表不存在相交节点，返回 null 。

图示两个链表在节点 c1 开始相交：

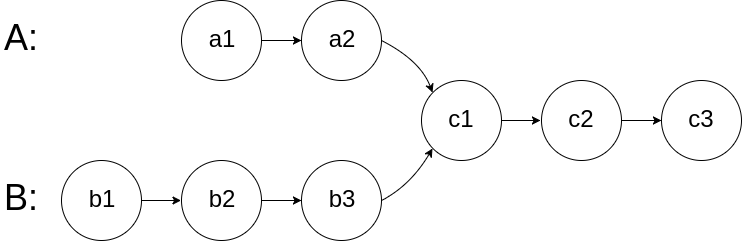
题目数据保证整个链式结构中不存在环。

注意，函数返回结果后，链表必须 保持其原始结构 。

自定义评测：

评测系统 的输入如下（你设计的程序 不适用 此输入）：

intersectVal - 相交的起始节点的值。如果不存在相交节点，这一值为 0
listA - 第一个链表
listB - 第二个链表
skipA - 在 listA 中（从头节点开始）跳到交叉节点的节点数
skipB - 在 listB 中（从头节点开始）跳到交叉节点的节点数

评测系统将根据这些输入创建链式数据结构，并将两个头节点 headA 和 headB 传递给你的程序。如果程序能够正确返回相交节点，那么你的解决方案将被 视作正确答案 。

示例 1：

输入：intersectVal = 8, listA = [4,1,8,4,5], listB = [5,6,1,8,4,5], skipA = 2, skipB = 3
输出：Intersected at '8'
解释：相交节点的值为 8 （注意，如果两个链表相交则不能为 0）。
从各自的表头开始算起，链表 A 为 [4,1,8,4,5]，链表 B 为 [5,6,1,8,4,5]。
在 A 中，相交节点前有 2 个节点；在 B 中，相交节点前有 3 个节点。
— 请注意相交节点的值不为 1，因为在链表 A 和链表 B 之中值为 1 的节点 (A 中第二个节点和 B 中第三个节点) 是不同的节点。换句话说，它们在内存中指向两个不同的位置，而链表 A 和链表 B 中值为 8 的节点 (A 中第三个节点，B 中第四个节点) 在内存中指向相同的位置。

示例 2：

输入：intersectVal = 2, listA = [1,9,1,2,4], listB = [3,2,4], skipA = 3, skipB = 1
输出：Intersected at '2'
解释：相交节点的值为 2 （注意，如果两个链表相交则不能为 0）。
从各自的表头开始算起，链表 A 为 [1,9,1,2,4]，链表 B 为 [3,2,4]。
在 A 中，相交节点前有 3 个节点；在 B 中，相交节点前有 1 个节点。

示例 3：


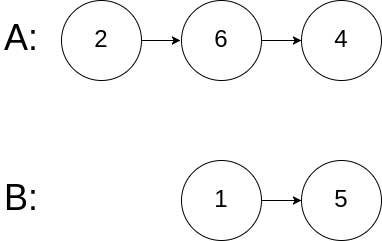
输入：intersectVal = 0, listA = [2,6,4], listB = [1,5], skipA = 3, skipB = 2
输出：No intersection
解释：从各自的表头开始算起，链表 A 为 [2,6,4]，链表 B 为 [1,5]。
由于这两个链表不相交，所以 intersectVal 必须为 0，而 skipA 和 skipB 可以是任意值。
这两个链表不相交，因此返回 null 。

提示：

listA 中节点数目为 m
listB 中节点数目为 n
1 <= m, n <= 3 * 104
1 <= Node.val <= 105
0 <= skipA <= m
0 <= skipB <= n
如果 listA 和 listB 没有交点，intersectVal 为 0
如果 listA 和 listB 有交点，intersectVal == listA[skipA] == listB[skipB]

进阶：你能否设计一个时间复杂度 O(m + n) 、仅用 O(1) 内存的解决方案？

思路 - 初见

初始思路：分开遍历，记录长度差，长的指针先走完差值，然后跟短指针一起走，找到交点或走完为止

代码 - 初见

public class Solution {
    public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
        // 1. 分别计算两个链表的长度
        int lenA = getLength(headA);
        int lenB = getLength(headB);
        
        // 2. 重置指针回到头节点
        ListNode pA = headA;
        ListNode pB = headB;
        
        // 3. 让长的指针先走 gap 步
        // 这样 pA 和 pB 距离尾部的长度就相等了（对齐起跑线）
        if (lenA > lenB) {
            int gap = lenA - lenB;
            while (gap-- > 0) pA = pA.next;
        } else {
            int gap = lenB - lenA;
            while (gap-- > 0) pB = pB.next;
        }
        
        // 4. 两人齐头并进，直到相遇
        while (pA != null && pB != null) {
            if (pA == pB) {
                return pA; // 找到交点
            }
            pA = pA.next;
            pB = pB.next;
        }
        
        return null; // 没有交点
    }
    
    // 辅助方法：计算链表长度
    private int getLength(ListNode head) {
        int len = 0;
        while (head != null) {
            len++;
            head = head.next;
        }
        return len;
    }
}

改进

🚀 方法二：更优思路（A+B = B+A）
虽然你的方法已经是 $O(N)$ 的最优解，但代码量稍多。
面试中还有一个非常巧妙的技巧，不需要显式计算长度差，被称为 “浪漫相遇法”。
思路：
指针 A 走完链表 A 后，直接跳到链表 B 的头继续走。
指针 B 走完链表 B 后，直接跳到链表 A 的头继续走。
原理：$Len_A + Len_B = Len_B + Len_A$。
只要它俩走的路程一样长，且速度一样，最后一定会在终点（交点）相遇。如果两个链表没有交点，它们会同时走到 null（相当于在终点相遇，只是终点是空）。

代码 - 改进

public class Solution {
    public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
        if (headA == null || headB == null) return null;
        
        ListNode pA = headA;
        ListNode pB = headB;
        
        // 只要不相等，就继续走
        // 哪怕没有交点，最后 pA 和 pB 都会同时变成 null，循环也会结束
        while (pA != pB) {
            // pA 走完了吗？走完了就去走 B 的路，否则继续走
            pA = (pA == null) ? headB : pA.next;
            
            // pB 走完了吗？走完了就去走 A 的路，否则继续走
            pB = (pB == null) ? headA : pB.next;
        }
        
        return pA;
    }
}

2 反转链表

难度：简单

思路 - 初见

头插法反转链表

class Solution {
    public ListNode reverseList(ListNode head) {
        // prev 代表“新链表”的头，一开始是 null
        ListNode prev = null;
        // curr 代表当前要处理的节点，一开始是原链表的头
        ListNode curr = head;
        
        while (curr != null) {
            // 1. 留后路：暂存当前节点的下一个节点
            // 因为下一步要断开 curr.next，不存就丢了
            ListNode nextTemp = curr.next;
            
            // 2. 头插动作：将当前节点指向新链表的头
            curr.next = prev;
            
            // 3. 更新新头：当前节点变成了新的“新链表头”
            prev = curr;
            
            // 4. 继续推进：处理原链表的下一个节点
            curr = nextTemp;
        }
        
        // 最后 prev 指向的就是反转后的新头节点
        return prev;
    }
}

3 回文链表

难度：简单

思路 - 初见

双指针，a走一步，b走两步，a一边寻找后半段链表一边反转前半段链表，反转完成后对比是否相同

class Solution {
    public boolean isPalindrome(ListNode head) {
        if (head == null || head.next == null) return true;

        ListNode slow = head;
        ListNode fast = head;
        ListNode prev = null; // 用于存储反转后的前半段链表头
        ListNode temp = null; // 临时变量用于交换

        // 1. 核心循环：快慢指针 + 前半段反转
        while (fast != null && fast.next != null) {
            // 1.1 快指针先走 (必须先走，否则slow反转后链表断了，fast回不去了)
            fast = fast.next.next;

            // 1.2 慢指针反转逻辑 (标准的头插法/反转逻辑)
            temp = slow.next; // 存下个节点
            slow.next = prev; // 回眸：当前节点指向前一个
            prev = slow;      // 更新头：prev 移到当前
            slow = temp;      // 走你：slow 移到下一个
        }

        // 2. 奇数长度处理 (关键细节)
        // 如果 fast 不为 null，说明链表长度是奇数
        // 此时 slow 正好停在正中间的那个节点上
        // 比如 1->2->3->2->1，此时 prev在左2，slow在3，fast在右1
        // 我们需要比较的是左2和右2，所以 slow 需要再走一步跨过中点
        if (fast != null) {
            slow = slow.next;
        }

        // 3. 对比前半段(prev) 和 后半段(slow)
        while (prev != null && slow != null) {
            if (prev.val != slow.val) {
                return false;
            }
            prev = prev.next;
            slow = slow.next;
        }

        return true;
    }
}

问题和改进

破坏链表结构后不好恢复
所以采用反转后半链表的方法（含恢复）
注：该方法时间上效率高，LeetCode击败100%的用户

代码 - 改进

class Solution {
    public boolean isPalindrome(ListNode head) {
        if (head == null || head.next == null) return true;

        // 1. 找到前半部分尾节点 (找中点)
        ListNode firstHalfEnd = endOfFirstHalf(head);
        
        // 2. 反转后半部分
        // 输入: 1->2->3->2->1
        // 变为: 1->2->3(end)    1->2(head) -> null (这里其实是 1->2(reversed))
        ListNode secondHalfStart = reverseList(firstHalfEnd.next);

        // 3. 判断是否回文
        ListNode p1 = head;
        ListNode p2 = secondHalfStart;
        boolean result = true;
        
        while (result && p2 != null) {
            if (p1.val != p2.val) {
                result = false;
            }
            p1 = p1.next;
            p2 = p2.next;
        }

        // 4. 恢复链表 (关键！再次反转后半部分)
        // 将 3 后面的部分再次反转，接回 3 后面
        firstHalfEnd.next = reverseList(secondHalfStart);
        
        // 5. 返回结果
        return result;
    }

    // 辅助函数：快慢指针找中点
    private ListNode endOfFirstHalf(ListNode head) {
        ListNode fast = head;
        ListNode slow = head;
        while (fast.next != null && fast.next.next != null) {
            fast = fast.next.next;
            slow = slow.next;
        }
        return slow;
    }

    // 辅助函数：反转链表
    private ListNode reverseList(ListNode head) {
        ListNode prev = null;
        ListNode curr = head;
        while (curr != null) {
            ListNode nextTemp = curr.next;
            curr.next = prev;
            prev = curr;
            curr = nextTemp;
        }
        return prev;
    }
}

4 环形链表

思路 - 初见

快慢指针，一个指针走一步，一个指针走两步，如果有环肯定会相遇

public class Solution {
    public boolean hasCycle(ListNode head) {
        // 1. 边界处理：空链表或只有一个节点不可能有环
        if (head == null || head.next == null) {
            return false;
        }
        
        // 2. 初始化快慢指针
        ListNode slow = head;
        ListNode fast = head;
        
        // 3. 开始赛跑
        // 只需要判断 fast 和 fast.next 是否为空
        // 因为 fast 跑得快，只要 fast 没掉下悬崖，slow 肯定也没事
        while (fast != null && fast.next != null) {
            slow = slow.next;       // 慢指针走 1 步
            fast = fast.next.next;  // 快指针走 2 步
            
            // 4. 相遇即有环
            if (slow == fast) {
                return true;
            }
        }
        
        // 5. 跑到了终点，说明没有环
        return false;
    }
}

问题和改进

🚀 进阶版：寻找环的入口 (LeetCode 142)
既然你已经掌握了相遇，面试中 90% 的概率会让你顺手把入环的第一个节点找出来。思路：这是数学推导的结果。
当 fast 和 slow 相遇时。
让其中一个指针（比如 fast）回到头节点 (head)。
另一个指针 (slow) 停在原地。
两个指针改为同速前进（都走 1 步）。
它们再次相遇的地方，就是环的入口。
数学原理速记（a = c）：
假设：
头到入口距离为 a
入口到相遇点距离为 b
相遇点回到入口距离为 c
相遇时：
慢指针走了 a + b
快指针走了 a + b + n(b+c) （多跑了 n 圈）
因为快指针速度是慢指针的 2 倍：2(a+b) = a + b + n(b+c)
化简得：a = (n-1)(b+c) + c
这说明：从头走 a 的距离，刚好等于从相遇点转圈圈最后走 c 的距离。

public class Solution {
    public ListNode detectCycle(ListNode head) {
        ListNode slow = head;
        ListNode fast = head;
        
        // 1. 先判断是否有环
        while (fast != null && fast.next != null) {
            slow = slow.next;
            fast = fast.next.next;
            
            if (slow == fast) {
                // === 这里的代码就是进阶部分 ===
                
                // 2. 相遇后，将 fast 重置回表头
                fast = head;
                
                // 3. 两个指针同时走 1 步，直到再次相遇
                while (slow != fast) {
                    slow = slow.next;
                    fast = fast.next;
                }
                
                // 4. 再次相遇点即为环入口
                return slow;
            }
        }
        
        return null; // 无环
    }
}

5 环形链表 II

难度：中等

思路代码（同上）

6 合并两个有序链表

难度：简单

思路 - 初见

两个指针分别指向头节点，不断把其中较小的结点连接到新的链表，直到其中一个链表为空

代码

class Solution {
    public ListNode mergeTwoLists(ListNode list1, ListNode list2) {
        // 1. 创建哨兵节点 (虚拟头节点)
        // 它的作用是作为一个固定的“桩子”，方便我们往后面挂节点
        ListNode prehead = new ListNode(-1);
        
        // prev 指针一直指向新链表的“尾巴”，负责连接新元素
        ListNode prev = prehead;
        
        // 2. 循环比较，直到其中一个链表为空
        while (list1 != null && list2 != null) {
            if (list1.val <= list2.val) {
                prev.next = list1;    // 接上 list1
                list1 = list1.next;   // list1 指针后移
            } else {
                prev.next = list2;    // 接上 list2
                list2 = list2.next;   // list2 指针后移
            }
            // 别忘了把 prev 指针也往后移一位，准备接下一个
            prev = prev.next;
        }
        
        // 3. 处理剩余部分 (关键点)
        // 循环结束时，肯定有一个链表还没走完。
        // 因为链表本身就是有序的，直接把剩下的那串“一锅端”接在后面就行
        // 不需要再写循环一个个接了，这是链表操作的优势 (O(1) 时间)
        prev.next = (list1 == null) ? list2 : list1;
        
        // 4. 返回哨兵节点的下一个，即真正的新链表头
        return prehead.next;
    }
}

7 两数相加

难度：中等

思路 - 初见

看起来似乎不难，尝试从两个链表的头节点开始相加，并记录进位情况和结果，然后插入到新链表中，直到其中一个链表为空，插入另一个链表剩余数与进位的和。

class Solution {
    public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
        // 创建哨兵节点（虚拟头节点），简化新链表的头节点处理
        ListNode dummy = new ListNode(0);
        ListNode curr = dummy;
        int carry = 0; // 记录进位

        // 只要 l1 或 l2 还有节点，或者还有进位没处理完，就继续循环
        // 这涵盖了“直到其中一个为空，插入另一个链表剩余数与进位的和”的所有情况
        while (l1 != null || l2 != null || carry != 0) {
            int x = (l1 != null) ? l1.val : 0;
            int y = (l2 != null) ? l2.val : 0;
            
            int sum = x + y + carry;
            
            // 更新进位
            carry = sum / 10;
            
            // 创建新节点存储当前位的结果 (sum % 10)
            curr.next = new ListNode(sum % 10);
            curr = curr.next;
            
            // 移动指针
            if (l1 != null) l1 = l1.next;
            if (l2 != null) l2 = l2.next;
        }

        return dummy.next;
    }
}

8 删除链表的倒数第 N 个节点

难度：中等

思路 - 初见

前后指针，后指针比前指针先走n次，然后前后指针一起走，后指针.next = null时，前指针.next = 前指针.next.next

需要哨兵节点来确保可以删除第一个节点

代码

class Solution {
    public ListNode removeNthFromEnd(ListNode head, int n) {
        // 1. 创建哨兵节点，指向 head
        // 作用：如果要删的是倒数最后一个节点（也就是正数第一个），
        // 有了 dummy，slow 就能停在 dummy 上，方便删除 head
        ListNode dummy = new ListNode(0, head);
        
        ListNode slow = dummy;
        ListNode fast = dummy;
        
        // 2. 让 fast 指针先走 n 步
        // 现在的状态：fast 和 slow 之间隔了 n 个节点
        for (int i = 0; i < n; i++) {
            fast = fast.next;
        }
        
        // 3. 两个指针一起走，直到 fast 走到最后一个节点
        // 注意循环条件：我们希望 slow 停在被删节点的前一个
        // 所以当 fast.next == null 时停止
        while (fast.next != null) {
            slow = slow.next;
            fast = fast.next;
        }
        
        // 此时：
        // fast 在最后一个节点
        // slow 在倒数第 n+1 个节点 (即目标节点的前驱)
        
        // 4. 删除倒数第 n 个节点
        slow.next = slow.next.next;
        
        return dummy.next;
    }
}

9 两两交换链表中的节点

难度：中等

思路 - 初见

双指针，后指针指向下一个需要交换的节点，前一个指针.next.next = 自己，然后自己.next = 后指针，前指针=后指针，后指针后移两位，直到后指针.next或者后指针.next.next = null

你的思路大体方向是对的（操作指针进行交换），但是描述中的逻辑“前一个指针.next.next = 自己”很容易导致链表断裂或者成环。
实现这道题最稳健的方法是引入一个 哨兵节点 (Dummy Node)，并使用 “三步走” 的策略来修改指针。
这里的核心难点在于：交换 A 和 B 时，不仅要修改 A 和 B 的指向，还需要修改 A 前面那个节点（prev）的指向。

代码

class Solution {
    public ListNode swapPairs(ListNode head) {
        // 1. 定义哨兵节点，简化头节点交换的逻辑
        ListNode dummy = new ListNode(-1);
        dummy.next = head;
        
        // temp 是每一对要交换节点的前驱节点 (Previous Node)
        ListNode temp = dummy;
        
        // 2. 循环条件：必须要后面至少有两个节点才能交换
        // temp.next 是第一个，temp.next.next 是第二个
        while (temp.next != null && temp.next.next != null) {
            // 3. 定义要交换的两个节点
            ListNode node1 = temp.next;
            ListNode node2 = temp.next.next;
            
            // 4. 开始交换 (三步走)
            // 第一步：前驱指向第二个节点 (dummy -> 2)
            temp.next = node2;
            
            // 第二步：第一个节点指向第三个节点 (1 -> 3)
            // 这一步非常关键，防止链表断裂，必须接上后面的部分
            node1.next = node2.next;
            
            // 第三步：第二个节点指向第一个节点 (2 -> 1)
            node2.next = node1;
            
            // 5. 指针后移
            // 现在的顺序是 dummy -> 2 -> 1 -> 3...
            // 下一对的前驱节点变成了 1 (也就是原来的 node1)
            temp = node1;
        }
        
        return dummy.next;
    }
}

10 随机链表的复制

难度：中等

思路 - 初见

暂无思路

🚀 锦囊二：拼接 + 拆分 (大神解法，空间 O(1))
这是本题的终极解法。不需要额外的 Map，我们利用链表本身的结构来存储映射关系。
核心技巧：原地复制（三步走）
第一步：原地克隆（复制身子）
把每一个新节点，插在原节点的后面。
原：A -> B -> C
变：A -> A' -> B -> B' -> C -> C'
妙处：现在 A 的下一个就是 A'，我们不需要 Map 也能立刻找到分身了！
第二步：搞定 Random（处理灵魂）
这是最关键的一步。
A 的 random 指向 C。
那么 A' (A.next) 的 random 应该指向哪里？当然是 C' (C.next)！
公式：curr.next.random = curr.random.next (如果 curr.random 不为空)
第三步：断开链表（分道扬镳）
把长链表拆成两个：
旧链表复原：A -> B -> C
新链表提取：A' -> B' -> C'

代码

/*
// Definition for a Node.
class Node {
    int val;
    Node next;
    Node random;

    public Node(int val) {
        this.val = val;
        this.next = null;
        this.random = null;
    }
}
*/

class Solution {
    public Node copyRandomList(Node head) {
        if (head == null) return null;

        // 1. 第一步：复制节点，并连接到原节点后面
        // A -> B -> null  =>  A -> A' -> B -> B' -> null
        Node curr = head;
        while (curr != null) {
            Node newNode = new Node(curr.val);
            newNode.next = curr.next; // 新节点先连上后面的
            curr.next = newNode;      // 旧节点连上新节点
            curr = newNode.next;      // curr 跳两步到下一个旧节点
        }

        // 2. 第二步：复制 random 指针
        curr = head;
        while (curr != null) {
            // 注意判空：如果旧节点的 random 是 null，新节点的 random 也是 null
            if (curr.random != null) {
                // 核心逻辑：新节点的 random = 旧节点 random 的 next (也就是 random 的分身)
                curr.next.random = curr.random.next; 
            }
            curr = curr.next.next; // 跳过新节点，去处理下一个旧节点
        }

        // 3. 第三步：拆分链表 (复原旧链表，提取新链表)
        curr = head;
        Node newHead = head.next; // 记下新链表的头
        Node copyCurr = newHead;

        while (curr != null) {
            // 复原旧链表: A -> B
            curr.next = curr.next.next;
            
            // 连接新链表: A' -> B'
            if (copyCurr.next != null) {
                copyCurr.next = copyCurr.next.next;
            }
            
            // 指针后移
            curr = curr.next;
            copyCurr = copyCurr.next;
        }

        return newHead;
    }
}

11 排序链表

难度：中等

思路 - 初见

🧠 核心思路：分治法 (Divide and Conquer)
这道题其实是你之前做过的两个题目的组合拳：
找中点（快慢指针，类似“回文链表”或“删除倒数节点”里的技巧）。
合并两个有序链表（你刚刚才做过的“拉拉链”）。
步骤（三部曲）：
切分 (Cut)：利用快慢指针找到链表中点，把链表一刀切断，变成两个子链表。
递归 (Recurse)：对左半边和右半边分别递归进行排序（直到只剩一个节点，它本身就是有序的）。
合并 (Merge)：将两个排好序的子链表合并成一个完整的有序链表。

代码

class Solution {
    public ListNode sortList(ListNode head) {
        // 1. 终止条件 (Base Case)
        // 如果链表为空，或只有一个节点，那它已经是有序的了，直接返回
        if (head == null || head.next == null) {
            return head;
        }

        // 2. 找中点并切断 (Cut)
        // 使用快慢指针。注意：fast 从 head.next 开始
        // 这样可以保证 slow 停在前半段的最后一个节点，方便切断
        ListNode slow = head;
        ListNode fast = head.next;
        
        while (fast != null && fast.next != null) {
            slow = slow.next;
            fast = fast.next.next;
        }

        // slow 是中点，midNext 是右半段的开头
        ListNode midNext = slow.next;
        
        // ⚠️ 关键动作：切断链表！否则会死循环
        slow.next = null; 

        // 3. 递归排序左右两半 (Recurse)
        ListNode left = sortList(head);
        ListNode right = sortList(midNext);

        // 4. 合并 (Merge) - 复用你之前的“合并两个有序链表”逻辑
        return merge(left, right);
    }

    // 辅助函数：合并两个有序链表 (你的拿手好戏)
    private ListNode merge(ListNode l1, ListNode l2) {
        ListNode dummy = new ListNode(-1);
        ListNode curr = dummy;
        
        while (l1 != null && l2 != null) {
            if (l1.val < l2.val) {
                curr.next = l1;
                l1 = l1.next;
            } else {
                curr.next = l2;
                l2 = l2.next;
            }
            curr = curr.next;
        }
        
        curr.next = (l1 != null) ? l1 : l2;
        return dummy.next;
    }
}

12 LRU缓存

难度：中等

思路 - 初见

LRU 缓存，定义一个map链表，头指针指向表头，以及count计数，put时，尾插法插入新数据，count++，大于容量时，删去头节点，get时，将get节点重新插入表的最后

你的思路大体上是对的！这就是标准的 “哈希表 + 双向链表” 解法。
为了实现 $O(1)$ 的时间复杂度，有几个关键点需要修正和细化：
必须是“双向”链表：因为当你 get 一个中间的节点时，你需要把它从当前位置删掉并移到尾部。如果是单向链表，删除当前节点需要遍历找到它的前驱，复杂度就是 $O(N)$ 了；而双向链表可以直接获得 prev，删除操作是 $O(1)$ 的。
哨兵节点 (Dummy Nodes)：为了避免频繁判断 head 或 tail 是否为空，我们通常建立两个虚拟节点：dummyHead 和 dummyTail。
dummyHead.next 是真正的最久未使用 (LRU) 数据。
dummyTail.prev 是真正的最近使用 (MRU) 数据。

代码

class LRUCache {

    // 1. 定义双向链表节点
    class DLinkedNode {
        int key;
        int value;
        DLinkedNode prev;
        DLinkedNode next;
        public DLinkedNode() {}
        public DLinkedNode(int key, int value) {
            this.key = key; 
            this.value = value;
        }
    }

    // 2. 核心变量
    private Map<Integer, DLinkedNode> cache = new HashMap<>();
    private int size;
    private int capacity;
    private DLinkedNode head, tail; // 哨兵节点

    public LRUCache(int capacity) {
        this.size = 0;
        this.capacity = capacity;
        
        // 初始化哨兵节点，避免边界判断
        head = new DLinkedNode();
        tail = new DLinkedNode();
        head.next = tail;
        tail.prev = head;
    }
    
    // 3. GET 操作
    public int get(int key) {
        DLinkedNode node = cache.get(key);
        if (node == null) {
            return -1;
        }
        // 如果存在，通过“移到末尾”标记为最近使用
        moveToTail(node);
        return node.value;
    }
    
    // 4. PUT 操作
    public void put(int key, int value) {
        DLinkedNode node = cache.get(key);
        
        if (node != null) {
            // 如果 key 存在，更新 value，并移到末尾
            node.value = value;
            moveToTail(node);
        } else {
            // 如果 key 不存在，创建新节点
            DLinkedNode newNode = new DLinkedNode(key, value);
            cache.put(key, newNode);
            addToTail(newNode); // 添加到末尾 (最新)
            size++;
            
            // 如果超容，删除头部节点 (最旧)
            if (size > capacity) {
                DLinkedNode lru = removeHead();
                cache.remove(lru.key); // 别忘了从哈希表中也删掉
                size--;
            }
        }
    }

    // ================= 辅助函数 (双向链表操作) =================

    // 移动节点到末尾 (等于先删除，再添加到末尾)
    private void moveToTail(DLinkedNode node) {
        removeNode(node);
        addToTail(node);
    }

    // 在链表尾部添加节点 (变成最新的)
    private void addToTail(DLinkedNode node) {
        // node 插入到 tail.prev 和 tail 之间
        node.prev = tail.prev;
        node.next = tail;
        tail.prev.next = node;
        tail.prev = node;
    }

    // 删除指定节点
    private void removeNode(DLinkedNode node) {
        node.prev.next = node.next;
        node.next.prev = node.prev;
    }

    // 删除头部真实节点 (即最久未使用的)
    private DLinkedNode removeHead() {
        DLinkedNode res = head.next;
        removeNode(res);
        return res;
    }
}

1 相交链表

题目描述

思路 - 初见

代码 - 初见

改进

代码 - 改进

2 反转链表

思路 - 初见

3 回文链表

思路 - 初见

问题和改进

代码 - 改进

4 环形链表

思路 - 初见

问题和改进

5 环形链表 II

思路代码（同上）

6 合并两个有序链表

思路 - 初见

代码

7 两数相加

思路 - 初见

8 删除链表的倒数第 N 个节点

思路 - 初见

代码

9 两两交换链表中的节点

思路 - 初见

代码

10 随机链表的复制

思路 - 初见

代码

11 排序链表

思路 - 初见

代码

12 LRU缓存

思路 - 初见

代码

分享文章

文章目录