1 移动零
难度:简单
题目描述
给定一个数组 nums,编写一个函数将所有 0 移动到数组的末尾,同时保持非零元素的相对顺序。
请注意 ,必须在不复制数组的情况下原地对数组进行操作。
示例 1:
输入: nums = [0,1,0,3,12]
输出: [1,3,12,0,0]1 <= nums.length <= 104-231 <= nums[i] <= 231 - 1
进阶:你能尽量减少完成的操作次数吗?
思路 - 初见
若存在0,移动之后恢复顺序必然存在其他数据的移动问题
从结果反推,若存在n个零,那最后n个元素不需要记录,改为0即可
遍历,记录0的个数,数字前面每存在m个0,就往前移m位
最后在末尾补m个0
代码 - 初见
class Solution {
public void moveZeroes(int[] nums) {
int zeroCount = 0;
// 第一遍遍历:统计0的个数并将非零元素前移
for (int i = 0; i < nums.length; i++) {
if (nums[i] == 0) {
zeroCount++; // 记录遇到的0
continue;
}
// 核心逻辑:当前索引 i 减去 0 的个数,就是该非零元素应该移动到的新位置
nums[i - zeroCount] = nums[i];
}
// 第二遍遍历:根据统计的 zeroCount,在数组末尾填充 0
for (int i = nums.length - zeroCount; i < nums.length; i++) {
nums[i] = 0;
}
}
}问题
上述代码已经可以很好的解决问题,但是缺乏显式双指针的可读性
代码 - 改进
class Solution {
public void moveZeroes(int[] nums) {
if (nums == null || nums.length == 0) return;
// j 指针:始终指向“下一个待填充非零元素”的位置
int j = 0;
// 1. 遍历数组,将非零元素依次放到 j 的位置
for (int i = 0; i < nums.length; i++) {
if (nums[i] != 0) {
nums[j] = nums[i];
j++; // 移动待填充位置
}
}
// 2. 将 j 之后的所有位置全部置为 0
// 此时 j 的数值正好是数组中非零元素的总数
while (j < nums.length) {
nums[j] = 0;
j++;
}
}
}2 盛最多水的容器
难度:中等
问题描述
给定一个长度为 n 的整数数组 height 。有 n 条垂线,第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。
找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
返回容器可以储存的最大水量。
说明:你不能倾斜容器。
示例 1:
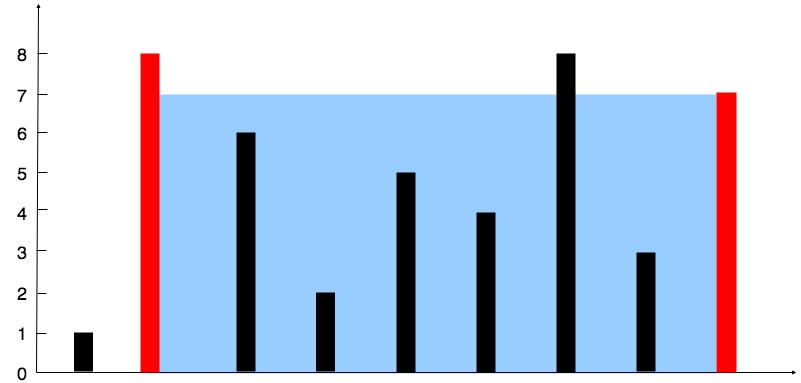

输入:[1,8,6,2,5,4,8,3,7]
输出:49
解释:图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下,容器能够容纳水(表示为蓝色部分)的最大值为 49。示例 2:
输入:height = [1,1]
输出:1
提示:
n == height.length2 <= n <= 1050 <= height[i] <= 104
思路 - 初见
双指针,分别指向两个线段,容量为底 × 高,底为指针下标差,高为短线段值
指针移动问题,假设极端情况,两端线段长为1,但是底长为6,中间线段为2*2,显然两端更大,反之亦然
一个思路,先找到两根最长的线段,然后指针慢慢外扩,寻找最大面积,怎么扩:比较两个线段旁边哪个更大###
代码 - 初见
class Solution {
public int maxArea(int[] height) {
int n = height.length;
if (n < 2) return 0;
// 1. 寻找全局最长的两根线段的下标 (原始思路第一步)
int firstMax = -1, secondMax = -1;
int firstIdx = -1, secondIdx = -1;
for (int i = 0; i < n; i++) {
if (height[i] > firstMax) {
secondMax = firstMax;
secondIdx = firstIdx;
firstMax = height[i];
firstIdx = i;
} else if (height[i] > secondMax) {
secondMax = height[i];
secondIdx = i;
}
}
// 确保 left 在左,right 在右
int left = Math.min(firstIdx, secondIdx);
int right = Math.max(firstIdx, secondIdx);
// 2. 初始面积
int maxArea = Math.min(height[left], height[right]) * (right - left);
// 3. 按照你的思路:指针慢慢外扩
// 只要左边还能往左,或者右边还能往右,就继续
while (left > 0 || right < n - 1) {
int leftVal = (left > 0) ? height[left - 1] : -1;
int rightVal = (right < n - 1) ? height[right + 1] : -1;
// 比较两边旁边哪个更大,往那边扩
if (leftVal > rightVal) {
left--;
} else {
right++;
}
// 更新面积
int currentArea = Math.min(height[left], height[right]) * (right - left);
maxArea = Math.max(maxArea, currentArea);
}
return maxArea;
}
}问题
局部最优陷阱:如果你先找到了两根最长的柱子,但它们离得很近(底边极短),而数组两端有两根中等长度但底边极长的柱子,你的扩散过程可能会因为中间遇到了几根“极短”的柱子,导致在扩散途中算出的面积一直很小,甚至可能错过真正的最优解(除非你遍历所有扩散路径)
输入:
height =[4,6,4,4,6,2,6,7,11,2]输出:
18预期结果:
42
起始点问题:如果最大值都在数组的左侧,那么“外扩”就无法触及右侧的区域。
改进逻辑:
初始状态:底最长。
移动逻辑:哪边高度短,就移动哪边。
原因:矩形的高度由短板决定。如果你移动长板,底边变短了,高度要么不变,要么变短,面积一定变小。只有移动短板,才有可能遇到更长的板,从而抵消底边缩短带来的损失。
代码 - 改进
class Solution {
public int maxArea(int[] height) {
int left = 0;
int right = height.length - 1;
int maxArea = 0;
while (left < right) {
// 计算当前面积
int currentArea = Math.min(height[left], height[right]) * (right - left);
maxArea = Math.max(maxArea, currentArea);
// 关键:移动较短的那一根
if (height[left] < height[right]) {
left++;
} else {
right--;
}
}
return maxArea;
}
}3 三数之和
难度:中等
问题描述
给你一个整数数组 nums ,判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i != j、i != k 且 j != k ,同时还满足 nums[i] + nums[j] + nums[k] == 0 。请你返回所有和为 0 且不重复的三元组。
注意:答案中不可以包含重复的三元组。
示例 1:
输入:nums = [-1,0,1,2,-1,-4]
输出:[[-1,-1,2],[-1,0,1]]
解释:
nums[0] + nums[1] + nums[2] = (-1) + 0 + 1 = 0 。
nums[1] + nums[2] + nums[4] = 0 + 1 + (-1) = 0 。
nums[0] + nums[3] + nums[4] = (-1) + 2 + (-1) = 0 。
不同的三元组是 [-1,0,1] 和 [-1,-1,2] 。
注意,输出的顺序和三元组的顺序并不重要。
示例 2:-
输入:nums = [0,1,1]
输出:[]
解释:唯一可能的三元组和不为 0 。
示例 3:
输入:nums = [0,0,0]
输出:[[0,0,0]]
解释:唯一可能的三元组和为 0 。
提示:
3 <= nums.length <= 3000-105 <= nums[i] <= 105
思路 - 初见
双指针+哈希,双指针确定前两个数,哈希定位最后的数
考虑指针移动策略,最后的三元组必含有一正一负
尝试从两端开始,移动绝对值大的那一个,这样剩下的值才可能落在中间
代码 - 初见
class Solution {
public List<List<Integer>> threeSum(int[] nums) {
// 为了方便使用“两端绝对值”策略,首先需要排序
Arrays.sort(nums);
Set<List<Integer>> result = new HashSet<>();
int left = 0;
int right = nums.length - 1;
// 原始思路:移动绝对值大的一端
while (left + 1 < right) {
int twoSum = nums[left] + nums[right];
int target = -twoSum;
// 在 [left + 1, right - 1] 区间内用哈希表找第三个数
// 这种做法不考虑性能优化,仅实现你的定位逻辑
Set<Integer> middleElements = new HashSet<>();
for (int k = left + 1; k < right; k++) {
middleElements.add(nums[k]);
}
if (middleElements.contains(target)) {
List<Integer> triplet = Arrays.asList(nums[left], target, nums[right]);
Collections.sort(triplet); // 确保去重有效
result.add(triplet);
}
// 指针移动策略:移动绝对值大的那一个
if (Math.abs(nums[left]) > Math.abs(nums[right])) {
left++;
} else {
right--;
}
}
return new ArrayList<>(result);
}
}问题
路径丢失:你的
while循环只走了一条从两端到中间的“唯一路径”。但在三数之和中,同一个left可能会对应多个不同的right和middle组合。重复计算:在循环内部重复创建
HashSet会导致效率极低,时间复杂度接近 O(n2)。改进:为了解决“路径丢失”的问题,标准的做法是:固定一个数,然后将其余两个数转化为“两数之和”问题。这样可以确保遍历所有可能的组合。
代码 - 改进
class Solution {
public List<List<Integer>> threeSum(int[] nums) {
List<List<Integer>> ans = new ArrayList<>();
if (nums == null || nums.length < 3) return ans;
Arrays.sort(nums); // 排序是基础
for (int i = 0; i < nums.length - 2; i++) {
// 如果当前数字大于0,后面三个数之和一定大于0,直接跳出
if (nums[i] > 0) break;
// 去重:如果此数与前一个数相同,跳过
if (i > 0 && nums[i] == nums[i - 1]) continue;
int L = i + 1;
int R = nums.length - 1;
while (L < R) {
int sum = nums[i] + nums[L] + nums[R];
if (sum == 0) {
ans.add(Arrays.asList(nums[i], nums[L], nums[R]));
// 去重:跳过相同的左值和右值
while (L < R && nums[L] == nums[L + 1]) L++;
while (L < R && nums[R] == nums[R - 1]) R--;
L++;
R--;
}
else if (sum < 0) L++; // 和太小,左指针右移
else if (sum > 0) R--; // 和太大,右指针左移
}
}
return ans;
}
}
